Polynomials | Class 10 Mathematics 2025 Best Notes

Polynomials | Class 10 Mathematics 2025 Best Notes

Polynomials

1. What is a polynomial?

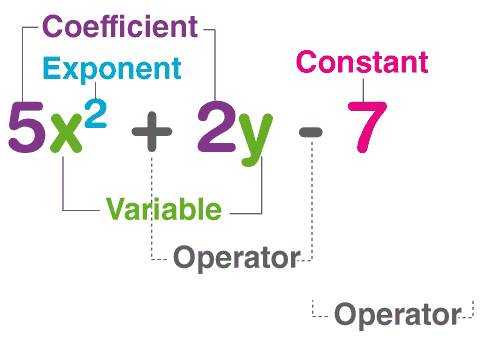
A polynomial p(x) in one variable x is an algebraic expression in x of the form P(x) = a_nxⁿ + a_n-1x^{n -1} + a_n-2x^n-2 + ………….. + a₂x² + a₁x + a₀, where x is a variable

1. a0, a1, a2 ……na are res pectively the coefficients of x0, x1, x2, x3, …… xn.
2. Each of a_nxⁿ, a_n-1 x^n-1, a_n-2x^n-2, ……… a₂x², a₁x, a₀, with a_n ≠ 0, is called the term of a polynomial.
3. The highest exponent of the variable in a polynomial determines the degree of the polynomial.
4. Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x² + x – 12. In this example, there are three terms: x2, x and -12.

The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial can have any number of terms but not infinite. Learn about degree, terms, types, properties, polynomial functions in this article.

• Types of polynomials
• A polynomial of degree zero is called a constant polynomial. Examples:
• A polynomial of degree one is called a linear polynomial. It is of the form ax + b.

Examples: x – 2, 4y + 89, 3x – z.

1. A polynomial of degree two is called a quadratic polynomial. It is of the form ax² + bx + c, where a, b, c are real numbers and a ≠ 0.

Examples: x² – 2x + 5, x² – 3x etc.

1. A polynomial of degree 3 is called a cubic polynomial and has the general form ax³ + bx² + cx +d.

For example: x3 + 2×2- 2x + 5 etc.

Monomial: A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:

• 5x
• 3
• 6a⁴
• -3xy

Binomial: A binomial is a polynomial expression which contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:

• – 5x + 3,
• 6a⁴ + 17x
• xy² + xy

Trinomial

A trinomial is an expression which is composed of exactly three terms. A few examples of trinomial expressions are:

• – 8a⁴ + 2x + 7
• 4x² + 9x + 7
• Value of the polynomial

If p(x) is a polynomial in x, and k is a real number then the value obtained after replacing x by k in p(x) is called the value of p(x) at x = k which is denoted by p(k).

• Zero of a polynomial
• A real number k is said to be the zero of the polynomial p(x), if p(k) = 0.
• Zeroes of the polynomial can be obtained by solving the equation p(x) = 0.
• It is possible that a polynomial may not have a real zero at all.
• For any linear polynomial ax + b, the zero is given by the expression (-b/a) = -(constant term)/(Coefficient of x).
• Number of zeroes of a polynomial
• The number of real zeros of the polynomial is the number of times its graph touches or intersects x- axis.
• The graph of a polynomial p(x) of degree n intersects or touches the x-axis at at most n points.
• A polynomial of degree n has at most n distinct real zeroes.
• A linear polynomial has at most one real zero.

Linear Polynomial having no zero.
Linear Polynomial having one zero.

• A quadratic polynomial has at most two real zeroes.

Quadratic Polynomial having no zeroes.
Quadratic Polynomial having one zero.
Quadratic Polynomial having two zeroes.

1. A cubic polynomial has at most three real zeroes.

Cubic Polynomial having no zeroes.
Cubic Polynomial having one zero.
Cubic Polynomial having one zeroes.
Cubic Polynomial having three zeroes.

1. Relationship between zeroes and coefficients of a polynomial:
2. For a linear polynomial ax + b, a ≠ 0, the zero is  It can be observed that:

1. For a quadratic polynomial ax² + bx + c, a ≠ 0,

Sum of the zeroes 

Product of the zeroes

1. For a cubic polynomial ax³ + bx² + cx + d = 0, a ≠ 0,

Sum of zeroes

Sum of the product of zeroes taken two at a time

Product of zeroes

1. The quadratic polynomial whose sum of the zeroes  and product of zeroes  is given by: k [x² – x + ], where k is real.

If a, b and g are the zeroes of a cubic polynomial f (x)= ax³ + bx² + cx + d, a¹ 0, then

f(x) = k (x – a)(x – b) (x – g)

f (x)= k {x³ – (a + b + g )x² + (ab + bg + ga )x – abg}, where k is any non-zero real number.

1. Process of dividing a polynomial f(x) by another polynomial g(x) is as follows:

Step 1: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor. Then carry out the division process.

Step 2: To obtain the second term of the quotient, divide the highest degree term of the new dividend by the highest degree term of the divisor. Then again carry out the division process

Step 3: Continue the process till the degree of the new dividend is less that the degree of the divisor. This will be called the remainder.

1. Division Algorithm for polynomials: If f(x) and g(x) are any two polynomials, where g(x) ≠ 0, then there exists the polynomials q(x) and r(x) such that f(x) = g(x) q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x)

So, q(x) is the quotient and r(x) is the remainder obtained when the polynomial f(x) is divided by the polynomial g(x).

1. Factor of the polynomial

If f(x) = g(x) q(x) + r(x) and r(x) = 0, then polynomial g(x) is a factor of the polynomial f(x).

1. Finding zeroes of a polynomial using division algorithm

Division algorithm can also be used to find the zeroes of a polynomial. For example, if ‘a’ and ‘b’ are two zeroes of a fourth degree polynomial f(x), then other two zeroes can be found out by dividing f(x) by (x-a)(x-b).

1. Properties

Some of the important properties of polynomials along with some important polynomial theorems are as follows:

Property 1: Division Algorithm

If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then,

P(x) = G(x) • Q(x) + R(x)

Property 2: Bezout’s Theorem

Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.

Property 3: Remainder Theorem

If P(x) is divided by (x – a) with remainder r, then P(a) = r.

Property 4: Factor Theorem

A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).

Property 5: Intermediate Value Theorem

If P(x) is a polynomial, and P(x) ≠ P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x, y].

Property 6

The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,

Degree (P ± Q) ≤ Degree (P or Q)

Degree (P × Q) = Degree (P) + Degree(Q)

Property 7

If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.

Property 8

If a polynomial P is divisible by two coprime polynomials Q and R, then it is divisible by (Q • R).

Important Questions

Multiple Choice questions-

1. If one zero of the quadratic polynomial x² + 3x + k is 2, then the value of k is

(a) 10

(b) -10

(c) 5

(d) -5

2. If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then

(a) a = -7, b = -1

(b) a = 5, b = -1

(c) a = 2, b = -6

(d) a – 0, b = -6

3. The number of polynomials having zeroes as -2 and 5 is

(a) 1

(b) 2

(c) 3

(d) more than 3

4. If one of the zeroes of the cubic polynomial x3 + ax² + bx + c is -1, then the product of the other two zeroes is

(a) b – a + 1

(b) b – a – 1

(c) a – b + 1

(d) a – b – 1

5. The zeroes of the quadratic polynomial x² + 99x + 127 are

(a) both positive

(b) both negative

(c) one positive and one negative

(d) both equal

5. The zeroes of the quadratic polynomial x² + kx + k, k? 0,

(a) cannot both be positive

(b) cannot both be negative

(c) are always unequal

(d) are always equal

6. If the zeroes of the quadratic polynomial ax² + bx + c, c # 0 are equal, then

(a) c and a have opposite signs

(b) c and b have opposite signs

(c) c and a have the same sign

(d) c and b have the same sign

7. If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it

(a) has no linear term and the constant term is negative.

(b) has no linear term and the constant term is positive.

(c) can have a linear term but the constant term is negative.

(d) can have a linear term but the constant term is positive.

8. The number of polynomials having zeroes as 4 and 7 is

(a) 2

(b) 3

(c) 4

(d) more than 4

9. A quadratic polynomial, whose zeores are -4 and -5, is

(a) x²-9x + 20

(b) x² + 9x + 20

(c) x²-9x- 20

(d) x² + 9x- 20

10. The zeroes of the quadratic polynomial x² + 1750x + 175000 are

(a) both negative

(b) one positive and one negative

(c) both positive

(d) both equal

        Very Short Questions:

1. What will the quotient and remainder be on division of ax² + bx + c by px² + qx² + rx + 5, p ≠ 0?
2. If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?
3. Can x – 2 be the remainder on division of a polynomial p(x) by x + 3?
4. Find the quadratic polynomial whose zeros are -3 and 4.
5. If one zero of the quadratic polynomial x² – 5x – 6 is 6 then find the other zero.
6. If both the zeros of the quadratic polynomial ax² + bx + c are equal and opposite in sign, then find the value of b.
7. What number should be added to the polynomial x² – 5x + 4, so that 3 is the zero of the polynomial?
8. Can a quadratic polynomial x² + kx + k have equal zeros for some odd integer k > 1?
9. If the zeros of a quadratic polynomial ax² + bx + c are both negative, then can we say a, b and c all have the same sign? Justify your answer.
10. If the graph of a polynomial intersects the x-axis at only one point, can it be a quadratic polynomial?
11. If the graph of a polynomial intersects the x-axis at exactly two points, is it necessarily a quadratic polynomial?

Short Questions :

1. If one of the zeros of the quadratic polynomial f(x) = 4x² – 8kx – 9 is equal in magnitude but opposite in sign of the other, find the value of k.
2. If one of the zeros of the quadratic polynomial (k – 1)x² + kx + 1 is -3 then find the value of k.
3. If 1 is a zero of the polynomial p(x) = ax² – 3(a – 1)x -1, then find the value of a.
4. If α and β are zeros of polynomial p(x) = x² – 5x + 6, then find the value of α + B – 3aß.
5. Find the zeros of the polynomial p(x) = 4x² – 12x + 9.
6. What must be subtracted from p(x) = 8x⁴ + 14x³ – 2x² + 7x – 8 so that the resulting polynomial is exactly divisible by g(x) = 4x² + 3x – 2?
7. What must be added to f(x) = 4x⁴ + 2x³ – 2x² + x – 1 so that the resulting polynomial is divisible by g(x) = x² + 2x – 3?
8. Obtain the zeros of quadratic polynomial 3x² – 8x + 4√3 and verify the relation between its zeros and coefficients.
9. If α and β are the zeros of the polynomial 6y2 – 7y + 2, find a quadratic polynomial whose zeros are  and .
10. If one zero of the polynomial 3x² – 8x + 2k + 1 is seven times the other, find the value of k.

Long Questions :

1. Verify that the numbers given alongside the cubic polynomial below are their zeros. Also verify the relationship between the zeros and the coefficients.

x³ – 4x² + 5x – 2; 2,1,1

• Find a cubic polynomial with the sum of the zeros, sum of the products of its zeros taken two at a time, and the product of its zeros as 2, -7, -14 respectively.
• Find the zeros of the polynomial f(x) = x3 – 5x² – 2x + 24, if it is given that the product of its two zeros is 12.
• If the remainder on division of x³ – kx² + 13x – 21 by 2x – 1 is -21, find the quotient and the value of k. Hence, find the zeros of the cubic polynomial x³ – kx² + 13x.
• Obtain all other zeros of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeros are  and  .
• Given that √2 is a zero of the cubic polynomial 6x³ + √2x² – 10x – 4√2, find its other zeros.
• If α, β, γ bezerosofpo1ynomial 6x³ + 3x² – 5x + 1, then find die value of α-1 + β-1 + γ-1.
• Find the zeros of the polynomial f(x) = – 12x² + 39x – 28, if it is given that the zeros are in AP.

Case Study Questions:

1. ABC construction company got the contract of making speed humps on roads. Speed humps are parabolic in shape and prevents overspeeding, minimise accidents and gives a chance for pedestrians to cross the road. The mathematical representation of a speed hump is shown in the given graph.

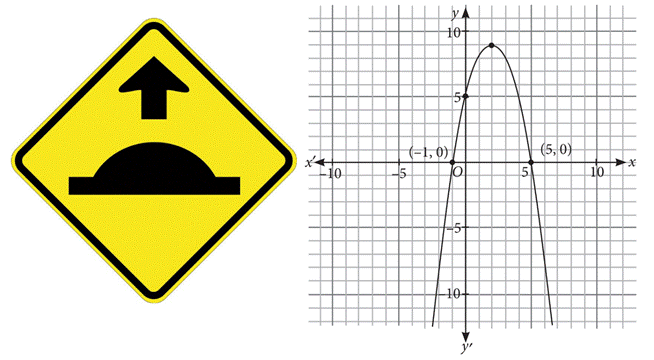
Based on the above information, answer the following questions.

1. The polynomial represented by the graph can be ____ polynomial.
2. Linear
3. Quadratic
4. Cubic
5. Zero
6. The zeroes of the polynomial represented by the graph are:
7. 1, 5
8. 1, -5
9. -1, 5
10. -1, -5
11. Sum of zeroes of the polynomial represented by the graph are:
12. 4
13. 5
14. 6
15. 7
16. If  and β are the zeroes of the polynomial represented by the graph such that β > , β > , then |8  + β| = |8  + β| =
17. 1
18. 2
19. 3
20. 4
21. The expression of the polynomial represented by the graph is:
22. x² – 4x – 5
23. x² + 4x + 5
24. x² + 4x – 5
25. -x² + 4x + 5
26. While playing in garden, Sahiba saw a honeycomb and asked her mother what is that. She replied that it’s a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is parabolic. The mathematical representation of the honeycomb structure is shown in the graph .

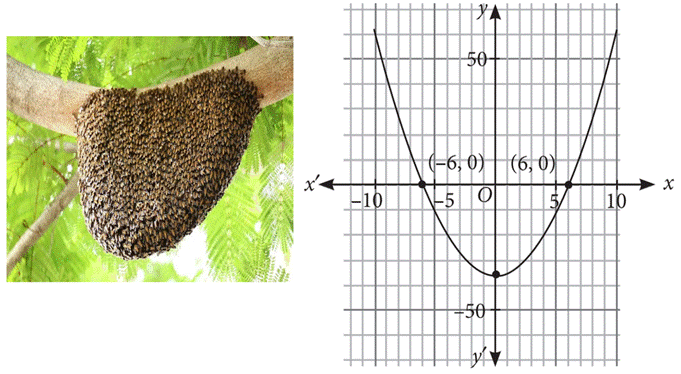
Based on the above information, answer the following questions.

1. Graph of a quadratic polynomial is _____ in shape.
2. Straight line.
3. Parabolic.
4. Circular.
5. None of these.
6. The expression of the polynomial represented by the graph is:
7. x² – 49
8. x² – 64
9. x² – 36
10. x² – 81
11. Find the value of the polynomial represented by the graph when x = 6.
12. -2
13. -1
14. 2
15. 1
16. The sum of zeroes of the polynomial x² + 2x – 3 is:
17. -1
18. -2
19. 2
20. 1
21. If the sum of zeroes of polynomial at² + 5t + 3a is equal to their product, then find the value of a.
22. -5
23. -3
24. 5353
25. −53−53

Assertion reason questions-

1. Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
2. Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
3. Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
4. Assertion (A) is true but reason (R) is false.
5. Assertion (A) is false but reason (R) is true.

Assertion: x² + 7x + 12 has no real zeroes.

Reason: A quadratic polynomial can have at the most two zeroes.

• Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
• Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
• Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
• Assertion (A) is true but reason (R) is false.
• Assertion (A) is false but reason (R) is true.

Assertion: If the sum of the zeroes of the quadratic polynomial x²-2kx+8 is 2 then value of k is 1.
Reason: Sum of zeroes of a quadratic polynomial ax²+bx+c is -b/a

Answer Key-

Multiple Choice questions-

1. (b) -10
2. (d) a – 0, b = -6
3. (d) more than 3
4. (a) b – a + 1
5. (b) both negative
6. (a) cannot both be positive
7. (c) c and a have the same sign
8. (a) has no linear term and the constant term is negative.
9. (d) more than 4
10. (b) x² + 9x + 20
11. (a) both negative

Very Short Answer :

1. 0, ax² + bx + C.
2. Since the quotient is zero, therefore

deg p(x) < deg g(x)

• No, as degree (x – 2) = degree (x + 3)
• Sum of zeros = -3 + 4 = 1,

Product of zeros = – 3 x 4 = -12

∴ Required polynomial = x² – x – 12

• Let α,6 be the zeros of given polynomial.

Then α + 6 = 5 3 ⇒ α = -1

• Let α and -α be the roots of given polynomial.

Then α + (-α) = 0 ⇒  = 0 ⇒ b = 0.

• Let f(x) = x² – 5x + 4

Then f(3) = 3² – 5 x 3 + 4 = -2

For f(3) = 0, 2 must be added to f(x).

• No, for equal zeros, k = 0, 4 ⇒ k should be even.
• Yes, because  = sum of zeros < 0, so that  = 0 > 0. Also the product of the zeros = = 0 > 0.
• Yes, because every quadratic polynomial has at the most two zeros.
• No, x⁴ – 1 is a polynomial intersecting the x-axis at exactly two points.

Short Answer :

1. Let one root of the given polynomial be α.

Then the other root = -α

Sum of the roots = (-α) + α = 0

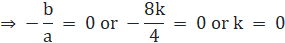
• Since – 3 is a zero of the given polynomial

∴ (k – 1)(-3)² + k(-3) + 1 = 0 :

⇒ 9k – 9 – 3k + 1 = 0 ⇒ k = 4/3.

• Put x = 1 in p(x)

∴ p(1) = a(1)² – 3(a – 1) x 1 – 1 = 0

⇒ a – 3a + 3 – 1 = 0 ⇒ 2a = -2 ⇒ a = 1

• Here, α + β = 5, αβ = 6

= α + β – 3αβ = 5 – 3 x 6 = -13

• p(x) = 4x² – 12x + 9 = (2x – 3)+

For zeros, p(x) = 0

⇒ (2x – 3)(2x – 3) = 0 ⇒ x =

• Let y be subtracted from polynomial p(x)

: 8x⁴ + 14x³ – 2x² + 7x – 8 – y is exactly divisible by g(x)

Now,

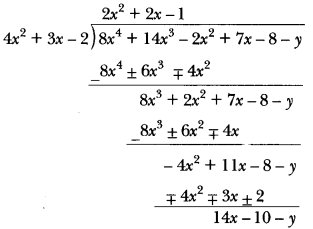
∵ Remainder should be 0.

∴ 14x – 10 – y = 0 or 14x – 10 = y or y = 14x – 10

∴ (14x – 10) should be subtracted from p(x) so that it will be exactly divisible by g(x)

• By division algorithm, we have

f(x) = g(x) × q(x) + r(x)

= f(x) – r(x) = g(x) × q(x) ⇒ f(x) + {-r(x)} = g(x) × q(x)

Clearly, RHS is divisible by g(x). Therefore, LHS is also divisible by g(x). Thus, if we add –r(x) to f(x), then the resulting polynomial is divisible by g(x). Let us now find the remainder when f(x) is divided by g(x).

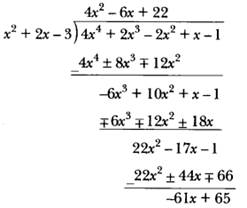
∴ r(x) = -61x + 65 or -r(x) = 61x – 65

Hence, we should add –r(x) = 61x – 65 to f(x) so that the resulting polynomial is divisible by g(x).

• We have,

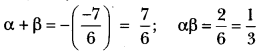
• Let p(y) = 6y² – 7y + 2

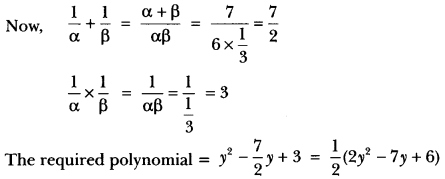
1. Let α and β be the zeros of the polynomial. Then as per question β = 7α

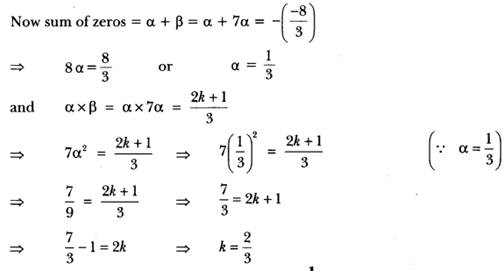
Long Answer :

1. Let p(x) = x³ – 4x² + 5x – 2

On comparing with general polynomial px) ax³ + bx² + cx + d, we get a = 1, b = -4, c = 5 and d = -2

Given zeros 2, 1, 1.

∴ p(2) = (2)³ – 4(2)² + 5(2) – 2 = 8 – 16 + 10 – 2 = 0

and p(1) = (1)³ – 4(1)² + 5(1) – 2 = 1 – 4 + 5 – 2 = 0

Hence, 2, 1 and I are the zeros of the given cubic polynomial.

Again, consider α = 2, β = 1, γ = 1

∴ α + 13 + y = 2 + 1 + 1 = 4

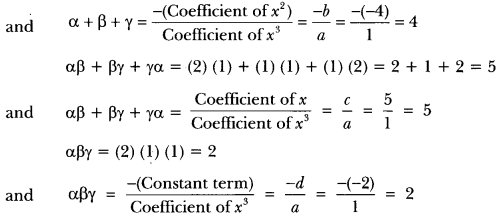
• Let the cubic polynomial be p(x) = ax³ + bx² + cx + d. Then

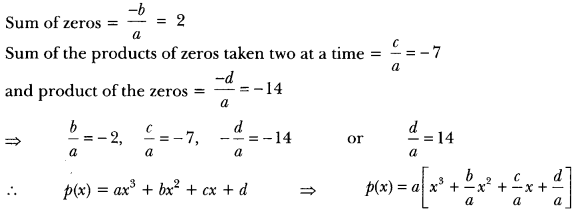
p(x) = a[x³ + (-2)x² + (-7)x + 14] ⇒ p(x) = a[x³ – 2x² – 7x + 14]

For real value of a = 1, p(x) = x³ – 2x² – 7x + 14

• Let α, β and γ be the zeros of polynomial (fx) such that αβ = 12.

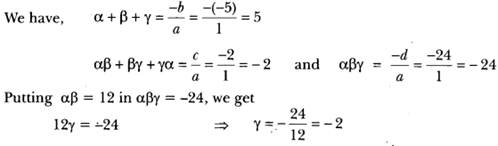
Now, α + β + γ = 5 α + β – 2 = 5

= α + β = 7 a = 7 – β

= (7 – β) β =12 ⇒ 7β – β² – 12

= β² + 7β + 12 = 0 ⇒ β² – 3β – 4β + 12 = O

= β = 4 or β = 3

β = 4 or β = 3

∴ α = 3 or α = 4

• Let f(x) = x³ – kx² + 13x – 21

•  

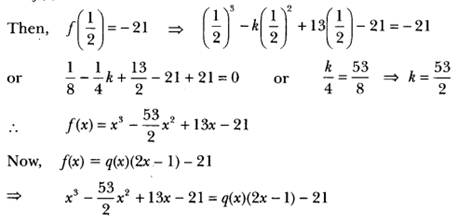
• The given polynomial is f(x) = (6x³ +√2x² – 10x – 4√2). Since √2 is the zero of f(x), it follows that (x – √2) is a factor of f(x).

On dividing f(x) by (x – √2), we get

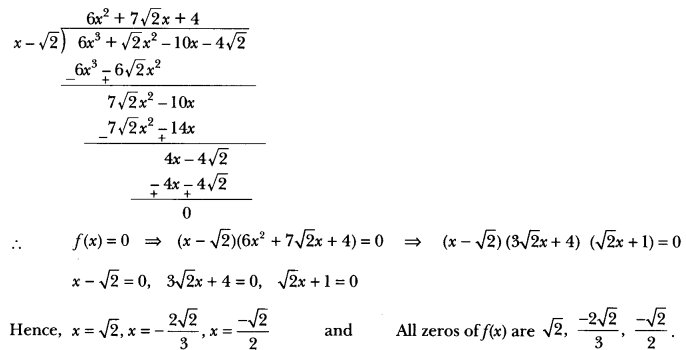
• ∵ p(x) = 6×3 + 3×2 – 5x + 1 so a = 6, b = 3, c = -5, d = 1

∴ α, β and γ are zeros of the polynomial p(x).

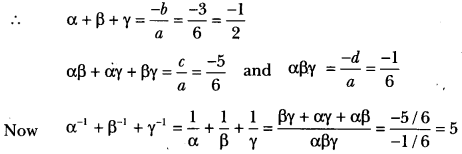
• If α, β, γ are in AP., then,

β – α = γ + β ⇒ 2β = α + γ

α + β + γ =  =  = 12 ⇒ α + γ = 12 – β …….. (i)

From (i) and (ii)

2β = 12 – β or 3β = 12 or β = 4

Putting the value of β in (i), we have

8 = a + γ

αβγ =  …….. (iii)

(αγ) 4 = 28 or αγ = 7 or γ = 7α ….. (iv)

Putting the value of γ = 7α in (iii), we get

⇒ 8 = α +  ⇒ 8α = α² + 7

⇒ α² – 8α + 7 = 0 ⇒ α² – 7α – 1α + 7 = 0

⇒ α(α – 7)-1 (α – 7) = 0 ⇒ (α – 1)(α – 7) = 0

⇒ α = 1 or α = 7

Case Study Answers:

1. Answer :
2. (b) Quadratic

Solution:

Since, the given graph is parabolic is shape, therefore it will represent a quadratic polynomial.

[∵ Graph of quadratic polynomial is parabolic in shape)

1. (c) -1, 5

Solution:

Since, the graph cuts the x-axis at -1, 5. So the polynomial has 2 zeroes i.e., -1 and 5.

1. (a) 4

Solution:

Sum of zeroes = -1 + 5 = 4

1. (c) 3

Solution:

Since α and β are zeroes of the given polynomial and β > α, β > α,

∴ α = -1 ∴ α = -1 and β = 5β = 5

∴ |8α + β| = |8(-1) + 5| = | -8 + 5| = |-3| = 3.

∴|8α + β|=|8(−1)+5|=|−8+5|=|−3|=3.

• (d) -x² + 4x + 5

Solution:

Since the zeroes of the given polynomial are -1 and 5.

∴ Required polynomial p(x)

= k² {x² – (-1 + 5)x + (-1)(5)} = k(x² – 4x – 5)

For k = -1, we get,

p(x) = -x² + 4x + 5, which is the required polynomial.

• Answer :
• (b) Parabolic.

Solution:

Graph of a quadratic polynomial is a parabolic in shape.

1. (c) x² – 36

Solution:

Since the graph of the polynomial cuts the x-axis at (-6, 0) and ( 6, 0). So, the zeroes of polynomial are -6 and 6.

∴ Required polynomial is

p(x) = x² – (-6 + 6)x + (-6)(6) = x² – 36

1. (c) 2

Solution:

We have, p(x) = x² – 36

Now, p(6) = 6² – 36 = 36 – 36 = 0

1. (b) -2

Solution:

Let f(x) = x² + 2x – 3. Then,

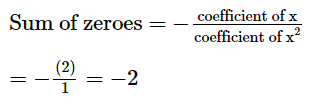
• (d) −53−53

Solution:

The given polynomial is at² + 5t + 3a

Given, sum of zeroes = product of zeroes

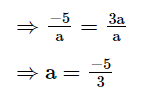
Assertion Reason Answer-

1. (d) Assertion (A) is false but reason (R) is true.
2. (a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).