Mathematics as Science of Logical Reasoning – Inductive Reasoning and – Deductive Reasoning- Reasoning is based on previous established facts. To establish a new fact or truth one has to put it on test of reasoning. If the new fact coincides with the previously established facts, it is called logical or rational. Logical reasoning is beyond subjectiveness. In the process of logical reasoning, we approach everything with a question mark in our mind. For each question we make a hypothesis and this hypothesis is tested empirically or theoretically with the help of previously proved or established truths or facts.
In mathematical working, we also move upwards by the process of reasoning. From our observation of physical and social environment, we form certain intuitive ideas or notions called postulates and axioms. These postulates and axioms are self-evident truths and need no further proof or explanation. Thus, postulates and axioms are assumed to be true without reasoning. But this does not mean that here we ignore the process of reasoning. Actually, self-evident truths are beyond reasoning.
That is why we can not assume any evidence to be true. Only those “evidences can be assumed as true that could not be proved untrue or irrational by existing logical knowledge. Thus, postulates and axioms are bases of mathematics as well as of our process of logical reasoning. In mathematics, we make several propositions and while proving a proposition we base our arguments on previously proved proposition. Thus, each proposition is supported by another proposition that has already been proved or established. Consequently if we go back one-by-one, we reach to a propositions that is based on postulates and axioms.
Mathematics as Science of Logical Reasoning – Inductive Reasoning and – Deductive Reasoning
Thus in mathematics we always use the process of logical reasoning. Therefore, mathematics may be called as the science of logical reasoning, In mathematics two types of reasoning are used. These prominent types of reasoning are
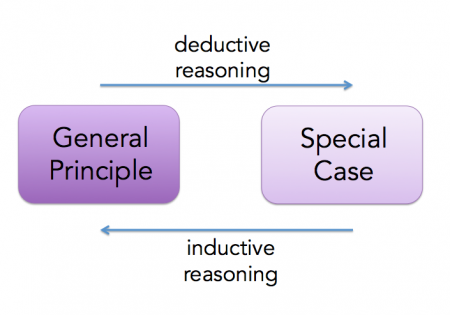
1. Inductive Reasoning and
2. Deductive Reasoning
Inductive Reasoning : Generally human knowledge arises from observations and experiences. In the beginning mathematics also arises out of practical applications and it is mostly inductive and intuitive. When the statements or propositions are based on general observations and experiences, the reasoning is called inductive. From our observation, we can get that some particular properties hold good in the sufficient number of cases and by this we may conclude that these properties will also hold good in all other similar cases. This type of logical reasoning is called inductive reasoning. Here inductive means that particular theme, theory, rule, formulae is induced from general experience or observation. Thus, in inductive reasoning we proceed from several particular examples or experiences to a general agreement. In mathematics this type of reasoning is very much used.
Deductive Reasoning : In deductive reasoning, We proceed from general to a specific. This type of reasoning is based on self-evident truth, established facts, postulates is proved with the help of already established general rules. Therefore in deductive reasoning we proceed from a premise. We make several statements or propositions in our mind. This reasoning consists in comparing the statements and drawing a conclusion therefrom. Thus, here we deduce the solution or proof of a particular problem or statement on the basis of a general premise. In mathematics, the inductive reasoning is useful for beginners but, afterward mostly deductive reasoning is more fruitful. As far as the place of inductive and deductive is concerned, the following saying is good enough to clear it.
Mathematics as Science of Logical Reasoning – Inductive Reasoning and – Deductive Reasoning
“Mathematics in the making is not a deductive science, it is an inductive, experimental science and guessing is the tool of mathematics. Mathematician like all other scientists, formulate their theories from bunches, analogies and simple examples. They are pretty confident that what they are trying to prove is correct, and in writing these, they use only the bull- dozer of logical deduction”.
Whitehead has also emphasized the importance of deductive reasoning in mathematics by saying, “Mathematics in its widest sense is the development of all types of deductive reasoning
, D’ Alembert says, “Geometry is a practical logic, because in it the rules of reasoning are applied in the most simple and sensible manner.”
Pascal says, “Logic has borrowed the rules of geometry. The method of avoiding error is sought by everyone. The logicians profess to lead the way, the geometers alone reach it, and aside from their science there is no true demonstration. Geometry is a true demonstration of logic. Mathematics is resources. As a conclusion the term science of teaching stands the only branch of knowledge, in which logical reasoning or for the ways and means provided to or utilized by a teacher for logical laws are applied and the results can be verified by the managing his task of teaching as smoothly and effectively as method of logical reasoning. possible by involving his least efforts for drawing the maximum.
Mathematics as Science of Logical Reasoning – Inductive Reasoning and – Deductive Reasoning
W.C.D. Whetham– “Mathematics is nothing but higher development of Symbolic Logic.
C.J. Keyser- “Symbolic Logic is Mathematics, Mathematics is Symbolic Logic.”
The symbols and methods used in the investigations of the foundation of mathematics can be transferred to the study of logic. They help in the development and formulation logical laws. In mathematics the symbol has got a meaning,
e.g., a < b means ‘a’ is less than ‘b’. In logic, the meaning of this symbol has been extended. Let ‘a’ denote the class denoted by the cows and ‘b’ stand for the class denoted by the animals, then a < b is easily interpreted to mean, “a is included in b” that is, all cows are animals.
For another example, take the symbol ‘x’. Let A denote the class, ‘Teachers’ and B the class, ‘Ladies.’ AXB may be interpreted to mean the class of persons who are both Teachers and Ladies. Thus the meanings of mathematical symbols have been extended to represent the relationship of propositions in logic.
The aims of the mathematician and those of the logician are practically the same.
.Mathematics as Science of Logical Reasoning – Inductive Reasoning and – Deductive Reasoning

